The Susskind Boost – String Theory
Angel Theory pt.1
M-Systems V4.03
By Nick Ray Ball from the 27th March to 20th May 2016

M-System 3. The Susskind Boost – String Theory – Leonard Susskind
The Susskind Boost is a quality of string theory as described by Professor Leonard Susskind, adapted into S-World network law, the Peet Tent and the GGW String.
M-Systems 0, 3 & 4
“The Susskind Boost V1.01>1.05
M-Research > V4a M-Systems part 1a 2016
Index
“The Susskind Boost” part 1.01- Lecture 1, String Theory, and M Theory
Condensed By Nick Ray Ball on about the 27th March 2016
Taken from
‘Leonard Susskind – Lecture 1, String Theory and M Theory’
Leonard Susskind: Lecture 1, String Theory, and M Theory
String Theory of Quantum Gravity
Leonard Susskind: Lecture 1, String Theory and M Theory
At 27 minutes
Its permissible to say that the string is full of gluons.
Imagine a rubber band, as you stretch it the number of molecules in it does not break and so eventually it brakes. But imagine a rubber band which as you stretch it, every time there was a gap opening between atoms, a new atom was inserted in-between. In that case, you could imagine that you could stretch this forever without braking it. And that’s the nature of the gluon field between a quark and an anti-quark. As you stretch it, the energy of stretching goes into creating more gluons.
Later At 34 Mins
Relativistic and Nonrelativistic Kinematics
We boost the hell out of the system along the Z axis (Profit axis). Until every single particle has a huge momentum along the Z axis.
If there is any particle that is going backwards along the Z access, you just have not boosted it enough. Just boost it more until its going forward with a large momentum.
The Energy is a sum of all the particles.
In the following P = Momentum, E = Energy and M = mass
All the momentum is in the PZ2 which is a constant.
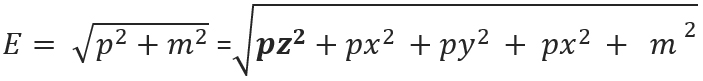
In this case, all of the pz’s are very large. What happens to px, py and m? when you boost something? Nothing? That’s the rest mass and the components of momentum perpendicular to the boost don’t change.
Quantum Mechanics and Time – If the energy of the system is very very small, then change takes place very, very slowly.
The more you boost a system, the slower it takes place.
In a very precise and exact way, the motion of a realistic system when its boosted up to enormously large momentum, behaves completely unrealistically. This is with respect to the motion in the plane perpendicular to the boost.
It is for this reason that String Theory is also often described in term of mathematics. Which is the mathematics of a nonrelativistic string.
An unrealistic string is a collection of particles
The motion of a string, when its boosted up, maybe described by a kind of nonrelativistic quantum mechanics.
Open String Theory is something with 2 ends (like a rubber band cut in half). There may or may not be something interesting attached to the ends. But we focus on the strings.
What is the energy stored in a string?
We can think of the string as a collection of points. Point particles which later we will (take) limit. One of the things we do when we take a limit is the mass of each point goes to zero. That’s because the whole string has a finite mass.
The energy of the string is proportional to its kinetic energy
Think of a string as a chain of little balls and springs,
1.05 minutes
Kinetic energy + Potential Energy (We have Marketing + Development energy) (Potential proportional to the stretching) (Adds up to all the internal motion in a particle) (Who’s to say that the object, the whole thing is not particles)
Kinetic is the relative motion of the different parts)
The overall motion of the string (the centre of mass of it) would just be treated as the position of the particle. But the relative stretching and the relative vibrations are internal energy
(Relative stretching and relative motion is internal energy).
The string in a rest state is equal to its mass squared m2
Which is the sum of all the energies within the string/particle.
A string is not so different to a spring. If you look at the spectrum of energies of a spring, its quantised in much the same way as a string.
A string is a collection of springs.
Each time you increase the energy of a spring or a string the internal energy by 1 unit, it increases the m2 by one unit.
We get from M to M2 by booting the string.
The rest mass is proportional to its length L=M
>>
2 kinds of strings Hooks Law and Flux Tube, which are related to each other. In one sense they are the same object described by 2 different reference frames. One at rest the other…..
Lots of field theories and condensed matter theories that have the same properties
Cool idea…
Higgs gives mass to particles and strings.
Energy of a string is M2, which we see as marketing and development, so the Higgs model is good, S-World gives its strings M2 and in exchange receives energy (money) which is used to Boost the system and give more M2 to the string.
Question for Susskind…
ou seem to start off with a classic string, then you boost it up.
The mass is proportional to the length.
It will create a smaller acceleration the larger the momentum
So in that way it’s easier to boost smaller or starter companies, so long as you have a good method for acceleration.
Inertia is the resistance of any physical object to any change in its state of motion (this includes changes to its speed, direction or state of rest). It is the tendency of objects to keep moving in a straight line at constant velocity.
1.41 minutes
Remarkably, the way String Theory works is that there are no independent degrees of freedom for motion along the other directions. This is a remarkable and strange fact, that in String Theory you do not include directly degrees of freedom, for the motion of the string along the direction of the boost.
It is thought that it is connected with something called the holographic principle. In a gravitating system you need one less direct dimension to describe it. You don’t describe the string in 3-dimensional space, you describe it in 2-dimensional motion.
To boost (or spin up) a hadron (big particle) does not take much because it’s a big particle, whereas proportionally the energy needed to boost a small particle like an electron. To spin up an atom needs only a couple of electron volts.
“The Susskind Boost” part 1.02 – The Susskind Boost, Plank Cubits & RES
By Nick Ray Ball 27th March 2016
Taken from
The Susskind Boost, Plank Cubits & The Clinton Equation
The Susskind Boost, Plank Cubits & The Clinton Equation
- 1. The Susskind Boost & Plank Cubits
A concept adapted from String Theory where If any company in the network is not in profit, we boost it! - 2. The Clinton Equation – RES Equation
Inspired by President Bill Clinton, how did he do it? The last great economic leader, the RES equation identifies the speed money circulates in a year a major factor within macroeconomics.
The network at the macro end is designed to give the brand power. Marketing and systems available to Fortune 100 companies to medium, small businesses and solo businesses. The basic is simply that given the same systems, 1 owner or partnership that owns a business will be more effective than one individual or pair of individuals that work for a business. For the same reason, why communism did not work in most countries as people work harder if the end result is to their own benefit.
The same would apply to a network of small businesses with many owners, stakeholders, CEOs and other high positioned staff in comparison to a large business, with only one incentivised person per 1000.
And such, for 5 years we worked on how to create a framework that gave the brand power. Marketing and systems to systems in our niche of hi end travel and property. We will soon have a significant website and we have planned 91 ways to boost the financial results from the software we are developing The Divergent CRM. And an addition 60 or so ways to boost any individual business in a string will improve due to the other businesses in the Network String. Which is 16 business.
In the Leonard Susskind Video: Leonard Susskind: Lecture 1, String Theory and M Theory
We see that within String Theory that the energy of a string is the sum of all the particles:
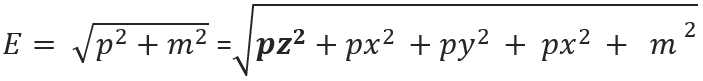
The motion of a string when its boosted up maybe described by a kind of nonrelativistic quantum mechanics.
To boost (or spin up) a hadron (big particle) does not take much because it’s a big particle, whereas proportionally the energy needed to boost a small particle like an electron.
As such within Angel Theory where we swop particles for business, the smaller a business within a string, the harder it is to boost. If the energy of the system is very very small, then change takes place very very slowly. And it is for this reason why it’s difficult for small businesses to succeed.
Hence, we can consider S-World as a system designed to boost small business to a point where they have the characteristics of larger businesses and so do not need as much attention.
In string theory, the energy of the points (businesses) within the string have both Kinetic energy + Potential Energy. In Angel Theory we can substitute Kinetic for Marketing and Potential as development (And note the RES equation supplies the Efficiency).
Boost It!
As such S-World has developed into a system that focuses on boosting the companies within its string and later strings of networks.
And due to the following quote, we know how best to handle any businesses that have fallen behind or requite assistance to lift off.
We boost the hell out of the system along the Z axis (Z can = Profit). Until every single particle (business) has a huge momentum.
If there is any particle (business) that is going backwards, you just have not boosted it enough. Just boost it more until its going forward with a large momentum.’
We Boost Them.
So far, within a string there are 16 companies all of which spend 25% of their Net Profit on contributions to indirect marketing, web, and software development. All companies use the same financial software so we can see the exact profitability of any company at any time. And so when we can see patterns that would lead to an unprofitable company we have plenty of time to react.
In an ideal world, it’s not so much about boosting companies that are not making profit. It’s about boosting any company that was not increasing profit. As all companies in a string are interlinked in many ways. A boost to the weakest will also have a positive effect on the entire string, making the entire string more profitable on mass.
But we also need to account for bad luck, depletion of resources, and the law of diminishing returns. So, when for some reason or another a company or a few companies within a string all fall into negative profit (make a loss), we fall back to the Susskind Boost and ‘Boost the hell out of them.’
Besides the 151 already recorded ways of boosting a company, tenders were the original Theory of Every Business Boost. In addition, a company may need to focus and develop itself in a different niche or one could see direct marketing from S-World into the company.
However there is another way, which twins with a way to initial boost new small companies that has been developing steadily over the years and that is Plank Cubits, the currency of the Network.
Plank Cubits & The Clinton Equation – RES Equation
In the first 4 books Plank Cubits hardly got a mention. Other than to say it made sense to try and peg the currency of the network to the plank length.
However, in both The Theory of Every Business and Quantum Economics a system of Network Credits was central to what we now call The Clinton Equation. Due to President Clinton being the last US president to create a profitable economy.
The Clinton Equation, or formally called the RES equation RES>100%, which says the initial input Revenue of the Network x Financial efficiency x Spin (the number of times the revenue is spent within a year must = over 100%, for the economy to grow).
Only after revisiting Lennard Susskind’s lecture and rediscovering the importance of the Susskind Boost did many parts of the same puzzle come together and create a model that could be used in the smallest of micro networks. The network as it is on 25th April 2016.
The Parts
- Is the point that we wished the currency of the network the Plank Cubit to take on the characteristics of bitcoin. In so much that if one bought 1 bitcoin at the time of its creation it would be worth thousands of times its original value today.But without the risk of it being used for buying illegal goods or money laundering.Or similar to a good stock option.
- We wanted it to be a constant, that could only change its value by doubling or halving.
- We want to create orders of goods from our luxury goods network ‘Lx.’
- We wish to reward clients, partners, and assistants in Plank Cubits.
- We want more and significant ways to apply the Susskind Boost.
- Eventually we want plank cubits to be owned by everyone and for the macroeconomic economic stimulus to also contribute, for all bonus to be paid in Network Credits. And still further in the future for business to business spending to be in Network Credits (Network Credits are plank cubits).The rules for plank cubits are never set, they can adapt at any timeCubits are a commodity not a currency, one cubit = an amount of Network Credits at any given time, they cannot be traded, and cannot be exchanged for cash.
The model is still in progress, but here is the first working model.
We don’t make Plank Cubits a currency, we make them a Network Credits exchange mechanism. Currently the network is tiny, and so Plank Cubits are not worth that much. They are worth as much as the Network can afford to give away in goods and services, divided by the amount on Cubits issued.
Currently the network can only afford $4,000 and maybe it will issue 8 Cubits. Exactly who gets the 8 cubits is not yet descried. However, as a particular client has helped fund Villa Secrets, helped suggest locations and helped with the webpages; I am already thinking of creating the guest’s gifts plan. Which would have given them the gift of a customised Lisa Marie Schneider handbag.
And in considering this, it was considered that instead of Cubits being an exchangeable currency, our clients would permanently own their cubit. Which will present various offers at various times. And we use the money spent to boost companies.
So in the case of our clients, their 1 Cubit would present an offer to spend $2,500 at Lx. Lisa Marie Schneider. Or alternatively $500 with Villa Secrets.
Offers need to be taken up within a fixed period of time, no extra money needs to be spent.
Basically, what we are doing is creating a boost, for the new company S-World ‘Lx’ by Lisa Marie Schneider. But as the network grows it can also be used to boost any company that is not in profit, or in general.
But in general, this system becomes the Network Credit system that we applied with great benefit to the network in Book 2 ‘Spiritually Inspired Software (Quantum Economics.) Where Network Credits worked in tandem with the spin of the Clinton Equation, to boost the network economics in general.
In the Macroeconomics this funding was created as a part of the POP Investment Principle. But now as Plank Cubits we get to deploy the power of the Clinton equation effectively to the Network at a micro level.
Here’s how it is currently considered, the network has $4,000 to spend on 8 plan cubits. But soon we expect to sell the network prototype for $200,000, and at which point the Network will be able to afford to issue $50,000 of Network Credits. Which will be shared between all the owners of Plank Cubits.
It’s likely we would issue an additional 24 plank cubits, creating a total of 32 plank cubits. Which will each split the network spend of $50,000 in Network Credits to the bearers of the Cubits. So about $1562 each. Which need to be spend within 4 months. So we know we will have $50,000 coming into the network in credits, which can be used to create and boost new business or be used to assist business that just need a boost.
The mechanism for how we create the Cubits increasing in value is not to increase the value, it is to issue more Cubits to those who already own Cubits.
So, for our clients, they will have received 1 of the first 8 Cubits, and an offer of $2,500 in S-World ‘Lx’ by Lisa Marie Schneider. But as the network grows it can also be used to boost any company that is not in profit, or in. Then when the next set of Cubits is issued they would receive a further offer of $1,562 x 5 in S-World ‘Lx’ by Lisa Marie Schneider (which they can use to buy gifts for friends). Plus, they would receive another Cubit. So they had 2 Cubits.
And on and on.
At the end of the day it matters not who has the Cubits, as the point of the exercise is to create ways to boost the network.
It would not take long, for the network to grow, and offer many services. Of which depending on how much one company or another needed a boost, more network credits would be on offer for the businesses that most needed a boost, stimulating the economy.
At a point, we could bridge the gap between the micro and macroeconomics by applying the Trump-Clinton Equation and Boosting the Spin, making it so that Network Credits needed to be spend within 4 weeks of issue.
We know from Book 2 Quantum Economics that we required a spin of about 3 or 4 times to create a healthy network economy. By tripling this speed, we create a super boost economy, which always looks first at new businesses and weaker businesses.
Of course, this principle only works if the network has enough money to exchange the Network Credits for cash for the companies within it. But the bigger the network, the more profit and the more people will pay to join it. And so it becomes circular.
And we add a new cost to the network, in the Network Credits it desires to give away.
For now, we are safe in the knowledge that certainly for the near future at the microscale the system works.
Of course, credits can be given to charities and the like for buying things they need as well.
“The Susskind Boost” part 1.03 – The Susskind Boost Equation.
By Nick Ray Ball 6th May 2016
Taken from
The Susskind Boost Equation (6th May 2016)
The Susskind Boost Equation
Ŝ = (Ḡ x ₰ x (Ѳ + Ś + Ś2 + ᶆ + ʧ )) x ϻ
The Susskind Equation is a part of POP: The Green-Hawking Algorithm (Ŝ x ϻ) x #□ = Ѫ
Unlike most other equations which are symbolic and better described as algorithm, I stand to be corrected. But it looks like this is an actual equation, and despite its hieroglyphic manner its actually very simple to understand.
Ŝ is the Susskind Boost and ϻ is the law of diminishing returns, most significantly market share. ϻ creates a percentage with lessens the effect of the Susskind Boost the closer one gets to market share saturation. (If the market for renting or selling property in a location is worth $100,000,000 the closer one gets to that figure, the greater boost is needed). So instead we create new strings in different locations and collectively boost them. Repeat, Repeat…
The Susskind Boost was as its name suggests inspired by Leonard Susskind, a pioneer, or even the creator of String Theory. One may find the exact point of reference for the Susskind Boost on the 1st of a series of lectures by Leonard Susskind for Stamford University called ‘Lecture 1 – String Theory and M-Theory‘
We start at 34 Mins.
Relativistic and Nonrelativistic Kinematics
‘We boost the hell out of the system along the Z axis, until every single particle has a huge momentum along the Z axis.
If there is any particle that is going backwards along the Z access, you just have not boosted it enough. Just boost it more until its going forward with a large momentum.’
(In our case the Z axis is net profit.)
This quote precisely described what we were trying to do in our real world company ‘Villa Secrets.’ At the time, we were considering how best to apply ‘The Amanda Stretch’ which is the way the String Feynman diagram could deal with the jitteriness and unpredictability of Quantum Mechanics, by stretching around all possible results.
With often 50% of profit available from each of the 8 particles (business) in our strings, we could by using the profit from all 7 strings deal with any given single failure. Or even the failure of a few but what was the best way to apply the profit from the other particles (business) to the failing company.
Before we go into this, a note that the financial software gives real time financials of all strings, so there are few surprises. However, small business can be effected by key staff leaving law suits, or other factors.
The consideration was if a company did go backwards, did we give direct financial assistance, or should we spend the money for additional marketing and development.
And on watching Leonard present the String Theory Boost, we not only knew that we should boost, not give money. But it also repositioned String Theory as at the centre of the math once more, and this time technically.
Different types of Susskind Boost.
First, the Susskind Boost is relative to the 2015 earnings and technology (or lack of technology) for prototype business Cape Town Luxury Villas, which made £70,000 in Gross Profit. And is currently in the process of being sold as a Villa Secrets network franchise for £110,000.
The boost is also relative to other conditions. Such as the industry type, the development of the industry type, and the development of the software amongst other factors. The following should also be considered up to. What may effect one company 400% could only effect another by 150%
- TFBM (Total Financial Business & Marketing) Software. Previously called (The Divergent CRM) adds about 400%.
If the full 400% was realised, gross profit would increase from £70,000 to £280,000Total up to Ŝ = 400% - Microbusiness structure creates very high owner/stakeholder vs paid employee ratio. A micro string of 8 companies may have 12 owners/stakeholders for 18 staff.
A standard string of 64 companies may have 100 owners and 200 staff
Add 200%Total up to Ŝ = 800% - The Ast⇔Bst, the effect of the other 7 companies in a micro string on the first company.
Currently we have 31 distinct points of positivity.
Add 200% moreTotal up to Ŝ = 1600% - The Ast2⇔Bst2 The effect of the other strings in the system (network) on the first string. No current model for this, but it will be big and get bigger and bigger
Add 200% moreTotal up to Ŝ = 3200% - Spending close to 50% of Net Profit on marketing and development is more than two times competing business.
Add 200%Total up to Ŝ = 6400% - 6. Lastly, for now we include the most powerful ‘booster’ the tender.
First considered in 2012 in the 2nd Chapter of The Theory of Every Business: The Suppliers Butterfly
Now practically considered for the first retail string ‘Lx.’ as a way to guarantee success even if the company does not make a single sale. The mechanism being the first 8 companies in the ‘Villa Secrets’ string dedicated 5% of Gross Turnover to ‘Lx.’ to supply handbags and jewellery to clients as gifts. The first practice example of ‘Economic Stimulus and Network Credits.’This powerful tender turns an uncertain niche into a guaranteed success, a very powerful boost. But it can only be used now and again as it takes a number of companies in a string to boost a single company in another.In terms of a percentage, to a degree its infinite, if it were the case that the company would not succeed without it. But for the sake of putting a value to it we shall say up to 200%Total up to Ŝ = 12800%
In addition, there are points that are relevant only if the physics are celebrated, such as PR (not from the physics rather what inspired the physics, Angel Sienna, the movie about Angel Sienna, the TV Series’ and the truck loads of philanthropy).
Plus, one should consider the Susskind Boost itself as a boosting mechanism.
And in addition the is the QuESC (Quantum Economic System Core), PQS (Predicative Quantum Software), S-World UCS (Universal Colonization Simulator) & UCS Voyager Simulations.
But currently we have 6 different types of boost. Let’s give them all a character
- TFBM Software = ₰ Changes to §
- Very high owner/stakeholder vs paid employee ratio = Ѳ
- Ast⇔Bst (Effects from other businesses in the string) = Ś
- Ast2⇔Bst2 (Effects from other strings in the network) = Ś2
- Spending close to 50% of Net Profit on marketing and development = ᶆ
- The tender = ʧ
Now we need to add some variables to each
- TFBM Software = ₰ Variables are:
- State of Completion
- Compatibility with industry
- Competitor development
- High owner/stakeholder vs paid employee ratio = Ѳ Variables are:
- Size of company
- Amount of times the company has created new companies and the ownership of the original owner in the new companies
- Effectiveness of owner
- Ast⇔Bst (Effects from other businesses in the string) = Ś Variables are:
- Synergy with other companies in the string
- Owners willingness to work with others
- Industry
- Ast2⇔Bst2 (Effects from other strings in the network) = Ś2 Variables are:
- Size of network
- Synergy with other strings in the network
- Industry
- The creation of other networks using a similar formula
- Spending close to 50% of Net Profit on marketing and development = ᶆ Variables are:
- The amount of Net Profit spent on marketing and development
- The amount of marketing and development paid for from company Net Profit
- The position the company is in compared to other companies in the string (if another company is being boosted due to Amanda Stretch less will be spent)
- The effectiveness of the marketing and development
- The tender = ʧ
- If a company has a tender
- The value of the tender
- The duration of the tender
- Industry
Ok, that’s 21 variables, there are many more. And the bigger the system gets the more variable there will be.
However, there is enough here to create a reasonable software program to assess the potential strength of the Susskind effect.
So
Ŝ = Initial Gross Profit x (₰ x (Ѳ + Ś + Ś2 + ᶆ + ʧ )) x % of ϻ
Let’s find a symbol for ‘Initial Gross Profit’ = Ḡ
Ŝ = (Ḡ x ₰ x (Ѳ + Ś + Ś2 + ᶆ + ʧ )) x % of ϻ
Actually
Ŝ = (Ḡ x ₰ x (Ѳ x Ś x Ś2 x ᶆ x ʧ )) x ϻ
By Nick Ray Ball 7th May 2016
How we apply the Susskind Boost
With the aid of a refresh of ‘String Theory for the Scientifically Curious with Dr. Amanda Peet.’ https://www.youtube.com/watch?v=PpQngpaHamg
We are now considering the Susskind Boost as a string with properties similar to the Higgs field.
First, I was already considering how we apply the Susskind Boost. And considering how we change the percentages of the model, its similar to the way a string changes from one particle to another. Which is not Higgs like, but it has Higgs properties as it gives boost to the other strings in the similar manner the Higgs gives mass.
Also like Villa Secrets and the rest of S-World, it does not have a profit centre. It’s only a reviver of money (energy) which 100% is output into boosting strings.
So let’s look at some different shapes off the Susskind string. In the prototype micro economic model S-Wold’s Villa Secrets.
In general, about 50% of net profit (25% of gross profit) (About 4.5% of turnover) is paid/donated to Villa Secrets. This money is then used to apply boost. First to the company that paid the money, then to its string of 8 companies and later in the form of POP (Ŝ x ϻ) x #□ = Ѫ it creates more strings in different locations.
The starting point we are considering for our first company Cape Town Luxury Villas is that all the money given to Villa Secrets is spent on boosting Cape Town Luxury Villas. Up to a set point of 2015 net profit x 33% ($100,000).
Actually the way the deal is being constructed it will also likely be 15% on net profit until $100,000. But this is mainly because I can’t show the reasons why it’s important to pay 25% due to this very point, the Susskind Boost.
However, we expect to work with 25% of Net Profit for the remaining 7 companies in the string. As we hope to have had some form of acknowledgement that the math is good from someone in physics.
Especially as it’s not a payment to a profit-making company. Depending on the state of the Susskind string its either going to return marketing and development with a value in excess of the cost. Or its going to be used for creating the software which in its self is a boost, but a boost to all. Or its going to be used to assist a company that has fallen behind, which is a bonus to any company from the start as it creates a zero failure rate. And as the network gets bigger and is respected for this quality, it will make the application for credit to buy a company in a string a lot more accessible. I expect we would find a bank who would finance just about anyone who was deemed to be of benefit to the network.
So there we have a different shape for the Susskind string. Where all the 25%’s of profit from the 7 string companies in a string, 7 x 25% of Net Profit, applying over 175% of the troubled companies total network profit into boosting the string and not taking the 25% from the troubled string. It would not take long for this string to recover.
We also have combinations. If in extreme circumstances 2 or 3 companies are not in profit, the 5 revenue companies in profit would be used to boost the 3 that were not.
However, in most cases, we would expect to have 8 profitable companies in a string.
In this case, I am considering a worst winners string. Where maybe 25% or 50% of the total that Villa Secrets receives is used to boost the 1,2 or 3 least profitable companies.
This really helps with the Amanda Stretch, (where we can boost our way out of any negative profit of a single company) as we are boosting the weakest winners, as so we are far less likely to need to apply the Amada Stretch in the first place.
As we saw in ‘POP’ (The Hawking-Green Equation (Ŝ x ϻ) x #□ = Ѫ ) in the classic and Baby POP examples we are also applying boost specifically to new companies, a string creates in another string. And this appears to be the most energy efficacy way of boosting the system as a whole, as we are no longest running into problems of market share.
And on this point, we have a very apt quote from Dr Amanda Peet.
So there’s obviously a law of diminishing returns, you crank up the energy to a point in string theory and you learn more information, but if you keep going and throw more money at the problem, nothing much interesting happens.
This is exactly why we added the ϻ to the Hawking-Green Equation (Ŝ x ϻ) x #□ = Ѫ
Lastly, there are some more fundamental rules we can apply to change the shape of the Susskind string, if considered as a whole as 8 x 25% of net profit so 200%. One can simply split this 200% into different destinations.
Maybe like this
- 50% into TFBM Software
- 50% into Boosting the 2 weakest companies in a string
- 25% into Boosting new companies in baby/different strings
- 25% into Economic Stimulus (guest gifts, staff loyally credits, tenders)
- 50% Network expansion (operations)
Adapting to circumstance and gaining efficiency with experience.
“The Susskind Boost” part 1.04 – String Theory fights Back – points 6 & 7
By Nick Ray Ball Between 15th and 20th May 2016
Taken from
“Angel Theory” part 1. M-Systems V2 – String Theory fights back! (20th May 2016)
6) The Susskind Boost
What is an initial condition and is set to 100% from the start is the Susskind Boost, which in principle was already a major factor in the S-World network design from 2011 to 2015.
However, when we revisited Professor Leonard Susskind’s (a pioneer of string theory) video Lecture 1 | String Theory and M-Theory we saw that our ‘all or nothing’ approach to marketing and development has precedent within string theory (and maybe other disciplines of physics) as Leonard Susskind presented at 34 minutes. (Note the words in brackets are to assist in seeing how we adapt the particle physics into economics).
‘We boost the hell out of the system along the Z axis (Profit axis). Until every single particle (company) has a huge momentum along the Z axis.
If there is any particle (company) that is going backwards along the Z access, you just have not boosted it enough. Just boost it more until its going forward with a large momentum.’
This not only fitted with our system. It also told us what to do with companies that went backwards, we just boost them some more.
We have an equation which is actually quite simple. It may look complex but that is due to us giving a different character to the different ways we can boost the system.
Ŝ = Ḡ x ( ʧ + Ŵ + Ƈ + Ѳ + Ś + Ś2 + ᶆ + ) x ҉ x %ϻ
Ŝ is the Susskind Boost and Ḡ is initial Gross Profit, which in the case of our 2015 prototype was about $100,000, so…
7. Ŝ =
8. Ḡ = $100,000
We multiply Ḡ this by the sum of 7 different types of boost that can affect our prototype. (Note the following is the projection for CTLV after three years. Each company has a different set of boosts. The bigger S-World Villa Secrets gets, the more boosting mechanisms there are.)
9. ʧ = Tenders = 75%
10. Ŵ = Additional Websites = 100%
11. Ƈ = Contracts or Mandates = 200%
12. Ѳ = High owner/stakeholder vs paid employee ratio = 50%
13. Ś = Ast⇔Bst Effects from other businesses in the string = 100%
14. Ś2 = Ast2⇔Bst2 Effects from other strings in the network = 100%
15. ᶆ = Spending close to 50% of Net Profit on marketing and development = 100%
16. ⃝ = Adding a Sun
17. ß = PR & Branding
18. ₪ = Links
19. Ǭ = QuESC
20. ₰ = S-World Virtual World (VSN)
21. ₰2 = S-World Virtual World (VBN)
22. ₱ = PQS
23. ₯ = PQS Voyager
24. ∫Ặ = Angel Cities
25. ҉ = TBMS
26. ⌂ = The Amanda Stretch
In the case of CTLV this equals a boost of 725%, which would change gross profit from $100,000 to $725,000.
Then we multiply the result by the completeness of the FTBMS software
27. ҉ = TFBM Software = 400% (See The Divergent CRM)
This leads to a potential boost of 2,900% in year 4, which would boost gross profit from $1,000,000 to $2,900,000.
However not all boosts are certain. For instance, ‘Ƈ ‘Contracts or Mandates assume the string as a whole will acquire between 50 and 100 joint mandates over 3 years. CTLV is measured as gaining 8, but it could gain more or less. In terms of certainty it’s a lot more certain that the string as a whole will collect between 50 and a 100. That it is to say which actual company will gain so many mandates.
Considering the string as a whole, if CTLV has the potential to grow its gross profit to $2,900,000 then we can reason that the string of 8 companies may make 8 times that figure $23,200,000. Which is a very good result. However, we need to consider market share, which is about $30,000,000. And so the string would need to gain 77% of market share, which is unrealistic.
So we need to add ‘ϻ’ a limiting factor for projections, following the law of diminishing returns, based on the size of the market in the first stage (1 to 3 years) and considering we should not (until there is precedent) project to over 25% of the market share. Not a complete wall, but making it about ten times harder to get past the ϻ of 25%. After 4 years we can increase ϻ
As such we restrict the growth potential of CTLV at about $950,000. Which is pretty much where we expect CTLV to be in 3 years’ time. And as a result we look at the factors within the Susskind Boost that are most economic or profitable and apply those first.
Later when we look at POP (The Pressure of Profit Investment Principle) and what we grandly call the ‘Hawking-Green Algorithm’ N x gs x (Ŝ x ϻ) = Ѫ, (named as such as it was created as a way to better present POP to both Professor Stephen Hawking and Professor Michael Green of Cambridge DAPTP).
N x gs x (Ŝ x %ϻ) = Ѫ,
In this algorithm/equation we will see how instead of trying to compete for more market share in one location when % ϻ is high, we instead create new strings in different locations where %ϻ is small and there is plenty of room in the market for a new set of hyper competitive players.
We are yet to add the component for the Amanda Stretch, Ặ it probably just fits in like so N x gs x (Ŝ x ϻ) x Ặ = Ѫ,
6b) How do we implement the Susskind Boost and how is it connected with the Amanda Stretch
First, we consider the Susskind Boost to be an intrinsic part of ‘Villa Secrets.’ It is a closed string that can operate in any location, which unless its laying the foundation for a new string does trade or make profit.
The 25% of gross profit that comes from the 8 companies in a string is used by Villa Secrets (and other such organizations in the same or different industries) to boost the network in the most efficient way possible, whilst holding on to the notion that no company can fail. We see the Susskind Boost as a string which changes shape to create different effects.
There will be many different models (shapes). However, at first the process is simple, as Professor Leonard Susskind says and experience has shown that it hardest to boost small systems. So, at first all the boost is directed at the company that contributes it. As such until the company has reached a specific point of gross profit (about 200% to 400% above the initial accepted expectations)
Once a company has been boosted enough, the Susskind Boost will split into different roles, and example of which follows:
- 25% of the boost from the entire string is focused on improving the TFBMS (Total Financial, Business & marketing Software) and the PQS (Predictive Quantum Software) as improvements in this increases the boost of all companies.
- 25% may be dedicated to operations, PR, media and content marketing which again boosts all companies
- 25% may be used as economic stimulus for a different industry string that can manufacture gifts for clients at great discount. The gifts created and given to top clients greatly increase the chances of repeat customers which boosts profit for all companies.
- 25% will be used to boost the two weakest companies in a string.It is the last 25% that greatly assists the Amanda Stretch (no company can fail) as if the weakest companies were effectively still seeing their 25% of gross profit used to boost their own companies. It’s very unlikely, given the initial conditions that any company in the string will ever fall out of profit and all will reach their POP point.
“The Susskind Boost” part 1.05 – The Susskind Boost Equation V1.04
By Nick Ray Ball 1st June 2016
Taken from
The Susskind Boost Equation V1.04 (1st June 2016)
The Susskind Boost Equation V1.04
I’m not sure about the pluses and multiplications, there are a lot of additional factors that could change things around. Like most of my equations, its actually more of a principle than an equation, a way to simply what would be millions of variables. So far with the TFBMS ₰ alone for just one company there are nearly a1000 variables.
So here it is in principle.

Ŝ = Ḡ x ₰ Ť + Ŵ + Ƈ + Ѳ + Ð + Ð2>9 + Ḿ – %ϻ – ⌂
I also listed all the variables, and changed a few symbols. Plus, I made a new to and from section for the percentages below. Note that in the main equation I only feature variables that are relevant to the current experiment at this time.
- Ť = Tenders or agency contracts = 0 to 200%
- Ŵ = Additional Websites = 0 to 400%
- Ƈ = Contracts or Mandates = 0 to 1000%
- Ѳ = High owner/stakeholder vs paid employee ratio = 0 to 200%
- Ð = Ast⇔Bst Effects from other businesses in the string = 0 to 250%
- Ð 2 = Ast2-9⇔Bst2-9 Effects from other strings in the network = 0 to 400%
- Ḿ = Spending +/-50% on marketing and development = 50% 150%
- ⃝ = Adding Gravity (One global brand per group/string) = 0% to 300%
- ß = PR & Branding After the physic has been published = 0% to 10,000
- ₪ = Links After the physic has been published = 50% to 750%
- Ǭ = QuESC Creating the network super-fast = 50% to 100%
- Ś = S-World Virtual World (VSN) = 100% to 500%
- Ś 2 = S-World Virtual World (VBN) = 100% to 500%
- ₯ = PQS Voyager = 50% to 350%
- Ăć Angel Cities = 200% to 20,000%
- Ḇr Brains – Membranes (7 global companies)
- ₱ = PQS
- ₰ = TFBM Software











Leave a Reply
Want to join the discussion?Feel free to contribute!